ישנן כמה דרכים למדוד את ה- עלויות ייצורוכמה מעלויות אלה קשורות בדרכים מעניינות. לדוגמה, עלות ממוצעת (AC), הנקראת גם עלות כוללת ממוצעת, היא העלות הכוללת מחולקת בכמות המיוצרת; עלות שולית (MC) היא העלות המצטברת של היחידה האחרונה שהופקה. להלן קשר בין עלות ממוצעת ועלות שולית:
אנלוגיה ליחס ממוצע ושולי עלות
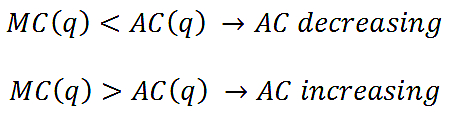
ג'ודי ביגס
ניתן להסביר בקלות את הקשר בין עלות שולי לממוצע באמצעות אנלוגיה פשוטה. במקום לחשוב על עלויות, חשוב על ציונים בסדרת בחינות.
נניח שהציון הממוצע שלך בקורס הוא 85. אם היית מקבל ציון של 80 בבחינה הבאה שלך, ציון זה היה מוריד את הממוצע שלך, והציון הממוצע החדש שלך יהיה משהו פחות מ 85. במילים אחרות, הציון הממוצע שלך יקטן.
אם היית קולע 90 בבחינה הבאה, ציון זה היה מגדיל את הממוצע שלך והממוצע החדש שלך יהיה משהו שמעל 85. במילים אחרות, הציון הממוצע שלך יגדל.
אם קיבלת 85 בבחינה, הממוצע שלך לא ישתנה.
בחזרה להקשר של עלויות ייצור, חשוב על עלות ממוצעת לכמות ייצור מסוימת כציון הממוצע הנוכחי ועלות שולית בכמות זו כציון בבחינה הבאה.
בדרך כלל אחד חושב על עלות שולית בכמות נתונה כעלות המצטברת הקשורה ליחידה האחרונה מיוצר, אך עלות שולית בכמות נתונה יכולה להתפרש גם כעלות המצטברת של הבא יחידה. הבחנה זו הופכת ללא רלוונטית בעת חישוב העלות השולית באמצעות שינויים קטנים מאוד בכמות המיוצרת.
בעקבות האנלוגיה לציון, העלות הממוצעת תרד בכמות המיוצרת כאשר העלות השולית הוא נמוך מהעלות הממוצעת ועולה בכמות כאשר העלות השולית גבוהה מהעלות הממוצעת. העלות הממוצעת לא תקטן ולא תעלה כאשר העלות השולית בכמות נתונה שווה לעלות הממוצעת באותה כמות.
צורת עקומת העלות השולית
ג'ודי ביגס
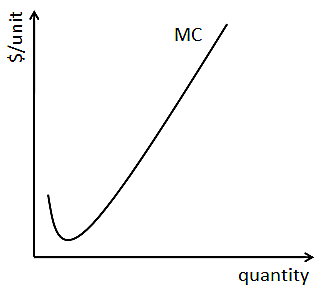
תהליכי הייצור של מרבית העסקים מסתיימים בסופו של דבר תוצר שולי פוחת של עבודה והפחתת התוצר השולי של ההון, מה שאומר שרוב העסקים מגיעים לנקודת ייצור בה כל יחידה נוספת של עבודה או הון אינה מועילה כמו זו שקדמה לה.
לאחר ההגעה למוצרים השוליים הפוחתים, העלות השולית לייצור כל יחידה נוספת תהיה גדולה מהעלות השולית של היחידה הקודמת. במילים אחרות, עקומת העלות השולית ברוב תהליכי הייצור תהיה בסופו של דבר מדרון כלפי מעלהכפי שמוצג כאן.
צורת עקומות העלות הממוצעת

ג'ודי ביגס
מכיוון שעלות ממוצעת כוללת עלות קבועה אך עלות שולית אינה עושה זאת, בדרך כלל המקרה הוא שהעלות הממוצעת גדולה יותר מעלות שולית בכמויות ייצור קטנות.
זה מרמז כי עלות ממוצעת בדרך כלל מקבלת צורה מסוג U, שכן העלות הממוצעת תקטן בכמות כל עוד העלות השולית נמוכה מהעלות הממוצעת אך אז תתחיל לגדול בכמות כאשר העלות השולית תהיה גדולה מהממוצע עלות.
קשר זה מרמז גם כי עלות ממוצעת ועלות שוליות מצטלבות במינימום עקומת העלות הממוצעת. הסיבה לכך היא שהעלות הממוצעת והעלות השולית נפגשות כאשר העלות הממוצעת עשתה את כל הירידה שלה אך טרם החלה לעלות.
הקשר בין עלויות משתנות וממוצע
ג'ודי ביגס
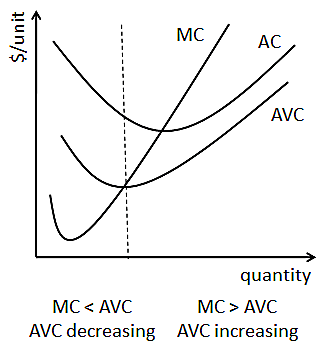
קשר דומה מחזיק בין עלות שולית לבין עלות משתנה ממוצעת. כאשר העלות השולית נמוכה מהעלות המשתנה הממוצעת, העלות המשתנה הממוצעת יורדת. כאשר העלות השולית גבוהה מהעלות הממוצעת הממוצעת, העלות המשתנה הממוצעת עולה.
במקרים מסוימים, משמעות הדבר היא גם כי עלות משתנה ממוצעת מקבלת צורה של U, אם כי הדבר אינו מובטח מכיוון שאף עלות משתנה ממוצעת או עלות שולית אינן מכילות מרכיב בעלות קבועה.
עלות ממוצעת למונופול טבעי
ג'ודי ביגס
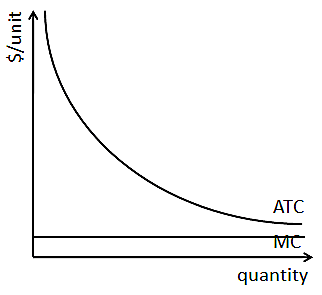
כי עלות שולית עבור מונופול טבעי לא עולה בכמות כפי שעושה בסופו של דבר עבור מרבית החברות, העלות הממוצעת מקבלת מסלול שונה עבור מונופולים טבעיים מאשר עבור חברות אחרות.
באופן ספציפי, העלויות הקבועות הכרוכות במונופול טבעי רומזות כי העלות הממוצעת גדולה יותר מהעלות השולית לכמויות ייצור קטנות. העובדה שעלות שולית למונופול טבעי אינה עולה בכמויות מרמזת כי העלות הממוצעת תהיה גדולה יותר מעלות שולית בכל כמויות הייצור.
משמעות הדבר היא כי במקום להיות בצורת U, העלות הממוצעת למונופול טבעי תמיד יורדת בכמות, כפי שמוצג כאן.